Ears for Pythagorean Harmonics Used to Investigate
"a Procrustean Group of Harmonies."

Introduction

Jean Piaget (1896-1980) was a pioneer psychologist of child development. In his "operational" model of intelligence, he established the importance of the algebraic group principle. The principle states that a person's activities often comply with the simple, compact system of rules defined for a mathematical object called a group. Compliance may be exact or approximate.

As a primal example, if a person can move freely in a space (e.g., a space of one, two or three dimensions), the movements of the person's body comply with the rules of an algebraic group. Chiefly, two movements, the second following upon the first, are equivalent in effect to a single movement; and any movement can be reversed, returning the body to the point of origin. The rules apply to movements of persons on a soccer field or walking along a street. They also apply to rotations of a wheel around an axis and to arithmetic.

The algebraic group principle organizes movements of other persons' bodies the same as one's own. In The Child's Construction of Reality (1937), Piaget shows how, in the first two years of life, each of us follows a path of intellectual development that leads toward such means of organization. Because the algebraic group principle is universal among persons, it supports objectivity and social order. "This organization of reality occurs, as we shall see, to the extent that the self is freed from itself by finding itself and so assigns itself a place as a thing among things, an event among events." Introduction at xiii. See also J. Piaget and B. Inhelder, The Psychology of the Child (1969) at 15-17 ("Space and Time"); H. Gruber and J. Voneche, eds., The Essential Piaget (1995), part VI ("Logico-Mathematical Operations").

Application of the algebraic group principle to the harmonic structure of Western music reveals a striking paradox. The principle applies to "well-tempered" music but only as a result of compromises and distortions involved in the "tempering." Although such music is entirely generated by human intelligence and evokes experience of the "ideal" and aspiration for the "ideal," the structure falls short of the ideal that would be expressed by a perfect algebraic group structure. Standard musical analysis describes the distortions and compromises using terms such as "Pythagorean comma." To make the structure of Western music fit the algebraic group principle, tones must be stretched or squeezed; and formerly pure, smooth harmonies acquire a rough and tense edge. (Classical North Indian music, e.g., ragas, avoids such problems by never modulating, as evidenced by "drone" tambura players who maintain tonic and perfect fifth tones throughout the performance.)

Stretching and squeezing the facts to fit a form is called "Procrustean" after the cruel bandit Procrustes, a figure in ancient Greek mythology who so tortured the limbs of his victims on an iron frame. I use the word to describe the way "natural harmonies" are stretched or squeezed to comply with the algebraic group principle.

This page presents advanced device designs based on "an Ear for Pythagorean harmonics." A series of developmental designs leads up to "full-scale Ears" which detect a complete set of harmonies in a musical scale and which can be used to investigate the mathematical basis of harmonic structure. The result is a tabular analysis of discrepancies as to the group closure principle. (Figure 15.) That principle would require that two harmonic steps, the second following on the first, must be equivalent to a single harmonic step. More than half the harmonic combinations in the table meet this requirement "perfectly" and are represented by a zero discrepancy -- "0." Other combinations result in small discrepancies under 1%; and there are also combinations with large discrepancies of over 3%.

The device designs show how a suitable "insensitivity" can be built into the detection system of the Ears. The "insensitivity" is defined as a specification of a timing device , namely "ξ" in Figure 1, the "rousal period" of a two pulse trigger device in a silence detector. Such insensitivity is varied and signals identified as Pythagorean harmonics switch on and off as such insensitivity passes through a particular value, which is the measure of the discrepancy.

[In terms of what we hear, a wobbly "beat" heard as roughness is generated by the simultaneous sounding of two tones that are very close. The "beat frequency" is the difference between the frequencies of the two underlying tones. If the beat frequency becomes "sufficiently" low, it is not heard and the two tones seem to be in "unison." In the Ears, such "sufficiency" is adjustable. A human violin player is especially well-trained to detect such roughness by ear, e.g., between his playing and that of his neighbors in the orchestra, and to adjust the position of his fingers on the strings to remove the discrepancy. In addition, there is vibrato, a quivering tone that results from a finger rocking back and forth; vibrato, like love, covers a multitude of sins.]

The fit between the constructed system of harmonies and the algebraic group principle is close but imperfect. I conjecture that the Ears, constructed by means of a subtraction principle, operate as an approximator to a logarithmic function, thus turning addition into multiplication and subtraction into division and ratios. If the fit were exact, a perfect algebraic group would have been established. However, the numbers don't quite work out...

...: link to web page and technical paper setting forth the foundational "Ear for Pythagorean harmonics." This page requires familiarity with the prior presentation.

Figure 13:  Table of gaps in group closure for harmonic combinations
(results from the first device design, using a pure tone approximation)

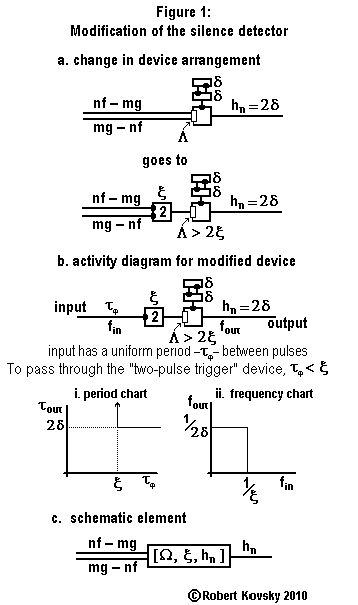
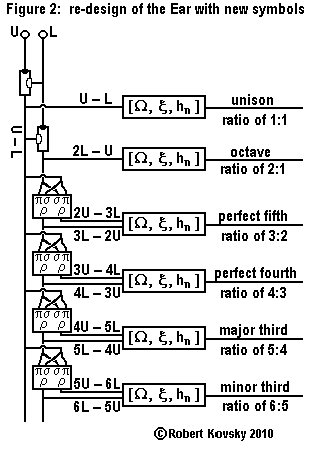
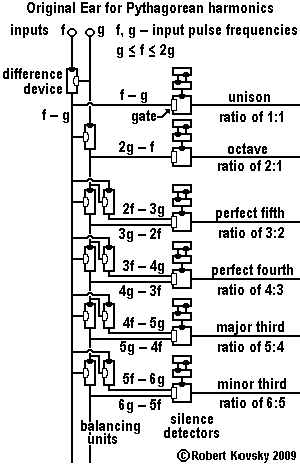
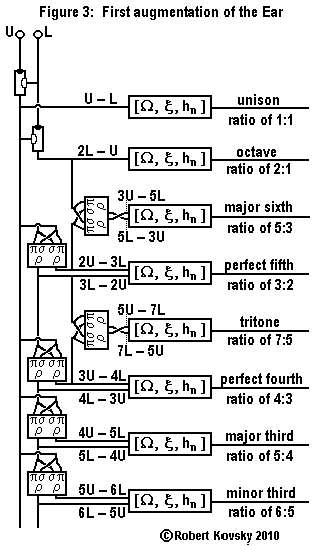
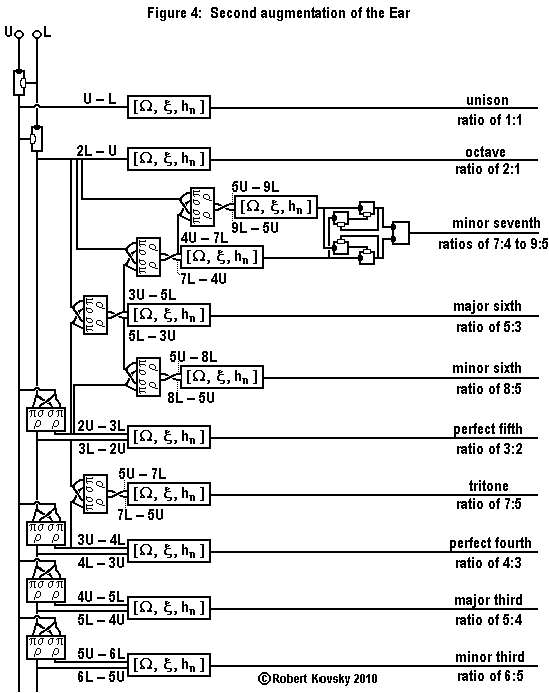
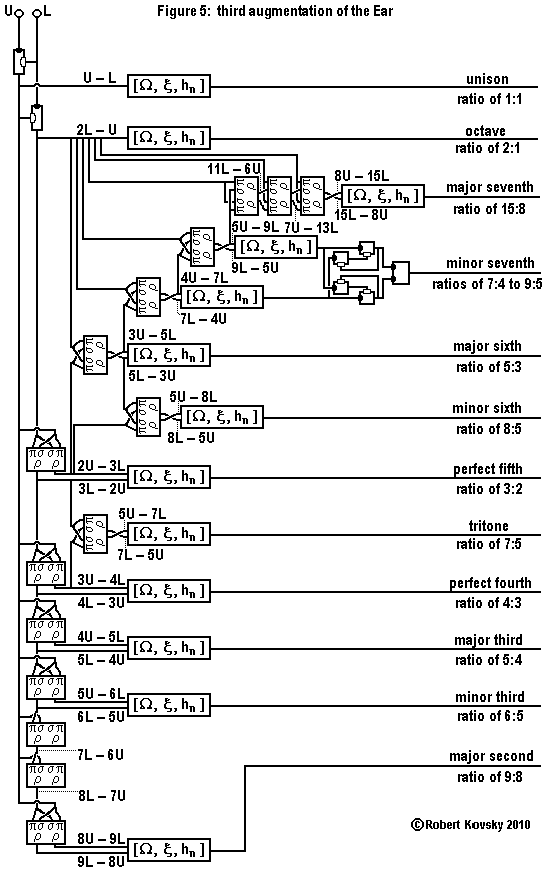
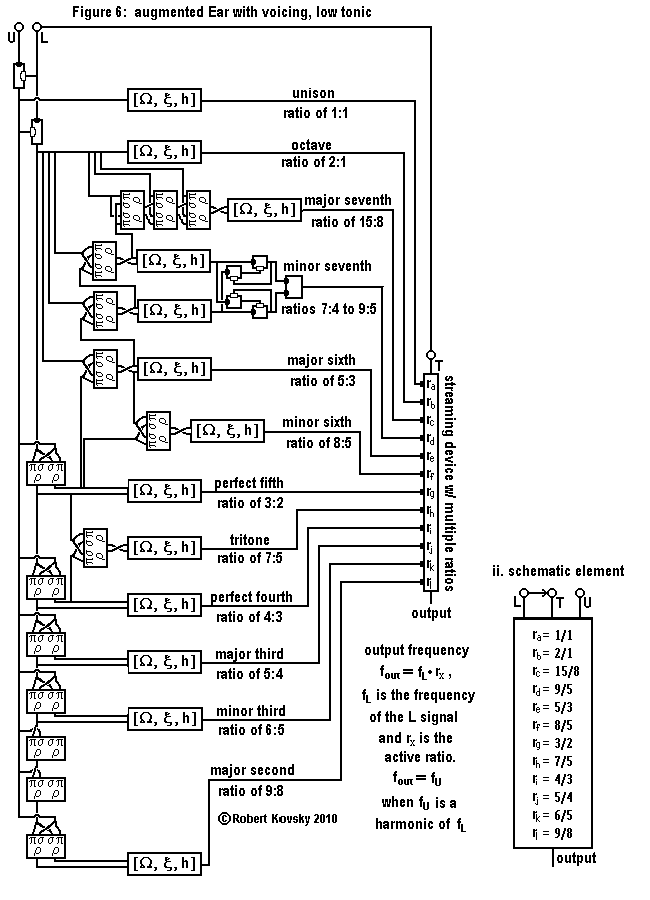
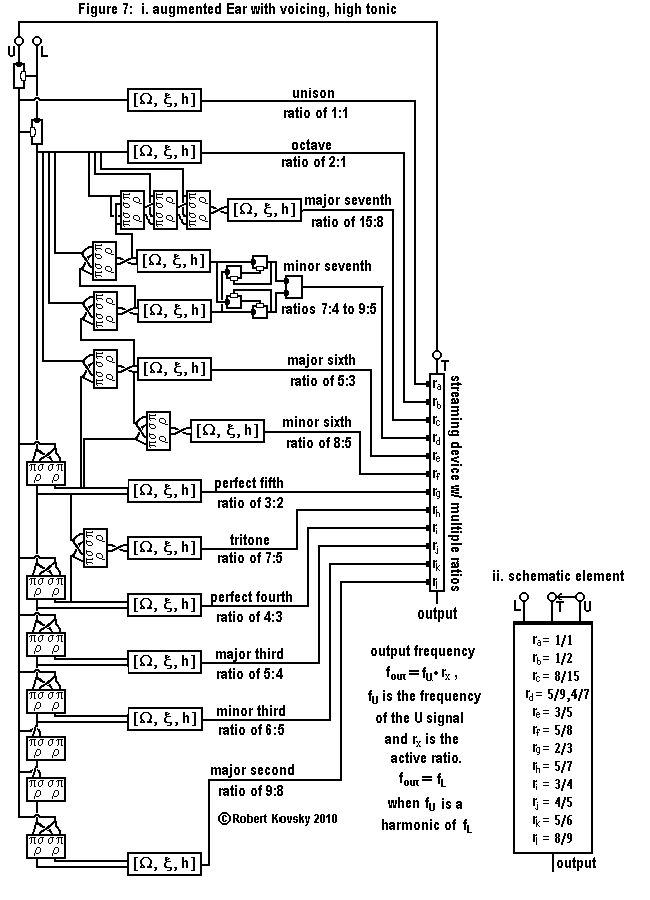
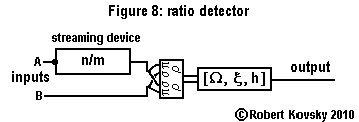
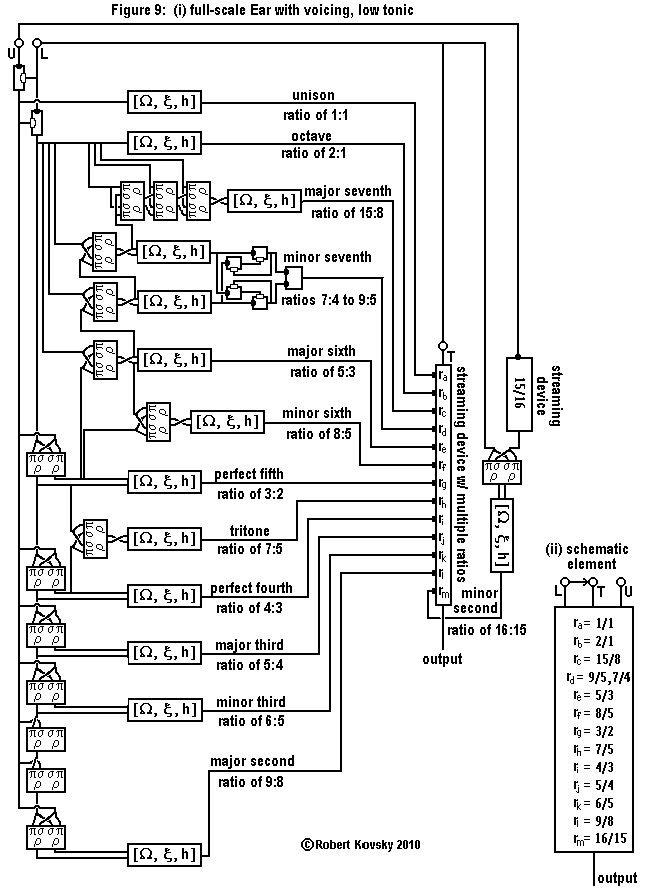
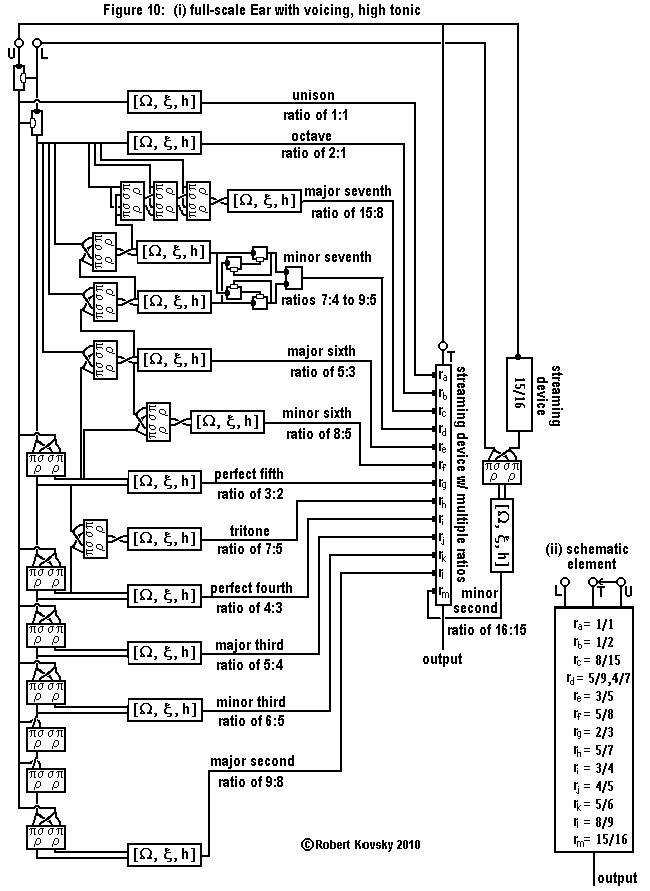
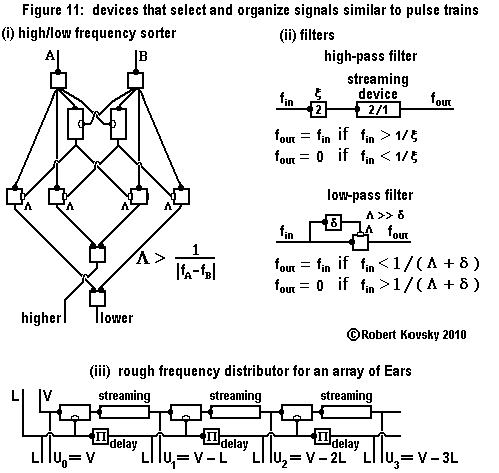
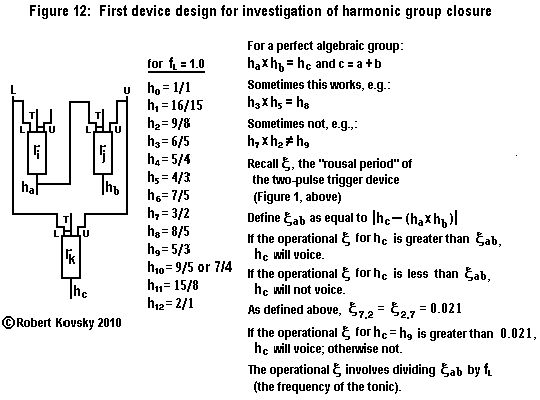
Table of limit values for
ξab = | hc - (ha x hb) |, where c = a + b and (ha x hb) < 2.
index   || 0 1 2 3 4 5 6 7 8 9 10 11 12
   hindex || 1 16/15 9/8 6/5 5/4 4/3 7/5 3/2 8/5 5/3 7/4
9/5 		15/8 2
— — — — — — — — — — — — — — — — — — — 
0 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0
1 16/15 | 0 0.013 0 0.030 0 0.022 0.007 0 0.040 0.023 0.008 0  
2 9/8 | 0 0 0.016 0.017 0.006 0 0.025 0.021 0 0      
3 6/5 | 0 0.030 0.017 0.040 0 0 0.013 0 0.045 0      
4 5/4 | 0 0 0.006 0 0.038 0 0 0 0        
5 4/3 | 0 0.022 0 0 0 0.023 0.008 0          
6 7/5 | 0 0.007 0.025 0.013 0 0.008 0.040            
7 3/2 | 0 0 0.021 0 0 0              
8 8/5 | 0 0.040 0 0.045 0                
9 5/3 | 0 0.023 0 0                  
10 7/4
9/5 		| 0 0.008                      
11 15/8 | 0 0                      
12 2 | 0                        

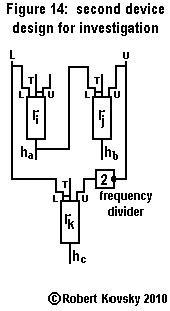
Figure 15:  Table of gaps in group closure for harmonic combinations
(combining results from both device designs and using a pure tone approximation)

Combined table of values for
ξab = | hc - (ha x hb) |, where c = a + b and (ha x hb) < 2; and
ξab = | hc - ½ (ha x hb) |, where c = a + b and (ha x hb) > 2.
index   || 0 1 2 3 4 5 6 7 8 9 10 11 12
   hindex || 1 16/15 9/8 6/5 5/4 4/3 7/5 3/2 8/5 5/3 7/4
9/5 		15/8 2
— — — — — — — — — — — — — — — — — — — 
0 1 | 0 0 0 0 0 0 0 0 0 0 0 0 0
1 16/15 | 0 0.013 0 0.030 0 0.022 0.007 0 0.040 0.023 0.008 0 0
2 9/8 | 0 0 0.016 0.017 0.006 0 0.025 0.021 0 0 0.012 0.012 0
3 6/5 | 0 0.030 0.017 0.040 0 0 0.013 0 0.045 0 0.013 0 0
4 5/4 | 0 0 0.006 0 0.038 0 0 0 0 0.025 0 0.028 0
5 4/3 | 0 0.022 0 0 0 0.023 0.008 0 0 0.014 0 0 0
6 7/5 | 0 0.007 0.025 0.013 0 0.008 0.040 0.017 0.005 0.033 0.010 0.021 0
7 3/2 | 0 0 0.021 0 0 0 0.017 0 0 0 0.017 0.006 0
8 8/5 | 0 0.040 0 0.045 0 0 0.005 0 0.030 0 0 0 0
9 5/3 | 0 0.023 0 0 0.025 0.014 0.033 0 0 0.011 0 0.038 0
10 7/4
9/5 		| 0 0.008 0.012 0.013 0 0 0.010 0.017 0 0 0.020 0.021 0
11 15/8 | 0 0 0.012 0 0.028 0 0.021 0.006 0 0.038 0.021 0.008 0
12 2 | 0 0 0 0 0 0 0 0 0 0 0 0 0

I have described myself in an author note on the earlier page.

Related Works by the Author

An Ear for Pythagorean Harmonics is part of the my larger work, where device designs for brains are the basis of a psychological model and the psychological model is used to investigate institutional activities, including physics and natural science, the laws of the courts and the Christian religion. The focus of interest in the larger work is personal freedom, especially as expressed through choices and selections made by persons in institutional situations. Of course, we exercise freedom in wilderness too, but institutional situations are more susceptible to analysis.

The engineering and scientific works set forth principles of device design that can be developed in several directions. Writings about psychological, philosophical, institutional, personal and spiritual matters are more tentative and even sketchy  – but they provide long-range motivation and have suggested particular inventions and pathways of development. For example, the design of the Ear for Pythagorean harmonics had its inception in my personal auditory investigations into "Duo Seraphim" by Claudio Monteverdi, discussed on the Shimmering Silences website, linked below.

I.    Engineering and Scientific Works
Quad Nets (2006)-- Quad Nets is the chief engineering and scientific presentation of my "device models of brains." Timing Devices, discussed here, began as a simplified version of the Quad Net Model.

Quad Nets website -- separately organized

web page on the full paper titled Quad Nets: Material Foundations for Thermal Device Models of Brains

download Quad Nets paper. (.pdf format, 1.1 Mb)
Timing Devices (2007-2009) has developed from a simplified version of the Quad Net Model into an independent area of investigation. The course of development includes possible future projects.

The complete Timing Devices paper is available for download, a .pdf file, 460 kB. Another web page presents the Abstract of the paper and the listing of Contents.

The separate website, link, Shimmering Silences in Beautiful Music (2009) presented initial investigations and original constructions that developed into the present Ear for Pythagorean Harmonics, along with an earlier version of the Timing Devices paper, titled An Ear for Pythagorean Harmonics: Mathematical Processing in Brain Models Built From "Timing Devices," (2009), a .pdf file 212 kB.

The separate web page, "Timing Devices or Why Brains Are Not Computers," link, is now the setting for the first, 2007, version of the Timing Devices paper, .pdf file, 363 kB.

The separate web page, Dancer - Shimmering Gaits of a Six-Legged Engineered Organism link, contains a proposed series of projects for construction of systems for engineered organisms (artificial animals) to be built from timing devices and Quad Net assemblies, starting with a "Utricle" that detects the orientation of an organism with respect to gravity and progressively leading upwards to a six-legged organism that uses a variety of coordination patterns ("gaits") in attempts to navigate a broken and obstructed terrain.

See also "Advanced Note: Convolution Timing Devices," a .pdf file (68 kB) link, preparatory for the present Timing Devices paper.

II.    Philosophy of Science
"Brains are computers" is part of a belief system that I call the Mechanical Cosmology and that includes other propositions: "all things are made of atoms" and "the Universe is governed by laws of physics, like the law of conservation of energy."

Beliefs about atoms and laws of physics have been developmentally productive and wonderfully fruitful in practical ways  – in contrast to "brains are computers"  – but they are also false and misleading. There are no "atoms." Atoms are mental constructions and they do not appear in reality. It is possible to buy materials, such as minerals, metals, refined chemical reagents, vegetable materials, animal materials and synthetic materials; but it is not possible to buy "atoms." The material that is closest to "atoms," refined helium, shows complex, collective, "non-atomic" properties when the temperature gets very low and the helium liquifies.

Energy is never "conserved." "Conservation of energy" is an ideal that is never attained, although billiard tables, vaccuum chambers and ball bearings rather approach it and make exact calculations possible under some circumstances.

Physicists believe that all of reality is made up of particles and laws of physics. Some parts of reality are well modeled by methods based on this belief but other parts of reality  – e.g., the reality of persons and the reality of conflicting principles of social organization  – cannot even be recognized. The physicists' belief is formed through study of imaginary conservative systems of atoms that can never be realized and that do not apply at all to situations that are most important to persons living their lives.

My works on these subjects are not as compactly organized as my engineering and scientific works and the themes run through many diverse works

Works related to Philosophy of Science

Please see a separate web page, "Facts About Snowflakes," about the generation of snowflakes from gaseous water vapor. Snowflakes can be beautifully symmetrical. Physicists are unable to account for this phenomenon because the proposed atomic processes are independent of one another and distant from each spatially. I argue that the attempt to explain the phenomenon by means of atomic processes is a failure. This failure is exemplary of the failures of physics to explain classes of phenomena of phase changes, of which the change from water to ice is the most familiar. I hold that important brain activities are phase changes and outside the reach of the Mechanical Cosmology. A Patchwork of Limits: Physics Viewed From an Indirect Approach (2000), a .pdf file (157 kB), is discussed on a separate web page The paper is a statement of my "alternative view of physics" that includes technical analysis of the thermodynamic critical state, the conceptual basis of Quad Nets.

A broad statement of my alternative view accessible to the lay reader, with a critical analysis of conventional physics, is in § 6 of "An Objective Kind of Freedom," an archival paper in the form of a .pdf file (618 kB.). The paper was published online in January of 2005 and the first six sections were foundational of my development of Quad Nets later in the year.

"On Cosmological Principles in Natural Science," a .pdf file (23 kB), link, is suggestive of future approaches.
(return to top of page).

III.    Large-scale Works

Testimony of Freedom
A separate website, under development, that establishes scientific and engineering foundations for investigations into social and spiritual matters.

Embodiment of Freedom
A separate website that was a prior stage of development, now superseded in large part by Testimony of Freedom. This site contains the Archive of my work that was done prior to May of 2005 and that led up to Quad Nets.

1/29/10 version

Copyright © 2010 Robert Kovsky