This page was originally published in 2007, was later amended, and continues to state chief principles in a useful way. Some later developments are listed ( ... ) below. All the pages on the site are listed in the ( ... ) Quad Net Site Map.

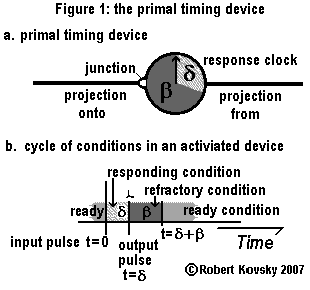 The primal timing device in Figure 1.a has a "response clock" shown in the form of a round clock dial. The response clock resembles a stopwatch used in a sports contest. It is controlled by two timing intervals: namely, δ, the responding period, and β, the refractory period. A timing interval is a period of time that governs the operations of a timing device and that is adjustable during operations. A timing interval or time period has a dimension of seconds, e.g., milliseconds.
Timing devices are interconnected by "projections." Timing devices are presently imaginary; in a supposed real device, a projection is a wire that conducts electricity or is "like" such a wire. A "projection from" extends out of a timing device and a "projection onto" attaches to a timing device through a "junction." A junction embodies the asymmetrical nature of a projection and resembles a synapse in a neuron. A projection from one timing device becomes a projection onto another timing device.
The primal timing device in Figure 1.a has a "response clock" shown in the form of a round clock dial. The response clock resembles a stopwatch used in a sports contest. It is controlled by two timing intervals: namely, δ, the responding period, and β, the refractory period. A timing interval is a period of time that governs the operations of a timing device and that is adjustable during operations. A timing interval or time period has a dimension of seconds, e.g., milliseconds.
Timing devices are interconnected by "projections." Timing devices are presently imaginary; in a supposed real device, a projection is a wire that conducts electricity or is "like" such a wire. A "projection from" extends out of a timing device and a "projection onto" attaches to a timing device through a "junction." A junction embodies the asymmetrical nature of a projection and resembles a synapse in a neuron. A projection from one timing device becomes a projection onto another timing device.
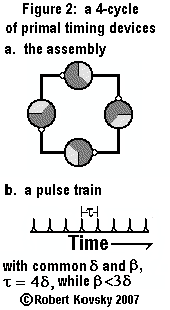 A 4-cycle made up of four primal timing devices. (Figure 2.a.) In the simplest form of the 4-cycle, all 4 timing devices have a common δ and β. During operations, each primal timing device produces pulses in a steady stream, called a pulse train, shown in Figure 2.b. The period between any two pulses in such a pulse train is τ=4δ. Operation of the 4-cycle requires that β<3δ. If β>3δ, a timing device will not have returned to the ready condition when the next input pulse arrives, which will, therefore, have no effect.
Suppose a 4-cycle is producing pulse trains while β<3δ. Then suppose that β is gradually increased until pulsing ceases as β passes upward through β=3δ. That is, a continuous variation in β causes a discontinuous change in the activity of the assembly. The activity of the 4-cycle is controlled by means of the ratio of β to δ. The control is in the nature of switch. In larger assemblies, small variations in timing intervals can cause an engineered organism to switch quickly between global modes of activity, e.g., like a switch from feeding to flight from danger. See § 5 of the Timing Devices paper, setting forth the design of a timing devices assembly called a "pulse period selector" that operates like a band-pass filter in electronics, where switching can be controlled by a small variation in a timing interval.
A 4-cycle made up of four primal timing devices. (Figure 2.a.) In the simplest form of the 4-cycle, all 4 timing devices have a common δ and β. During operations, each primal timing device produces pulses in a steady stream, called a pulse train, shown in Figure 2.b. The period between any two pulses in such a pulse train is τ=4δ. Operation of the 4-cycle requires that β<3δ. If β>3δ, a timing device will not have returned to the ready condition when the next input pulse arrives, which will, therefore, have no effect.
Suppose a 4-cycle is producing pulse trains while β<3δ. Then suppose that β is gradually increased until pulsing ceases as β passes upward through β=3δ. That is, a continuous variation in β causes a discontinuous change in the activity of the assembly. The activity of the 4-cycle is controlled by means of the ratio of β to δ. The control is in the nature of switch. In larger assemblies, small variations in timing intervals can cause an engineered organism to switch quickly between global modes of activity, e.g., like a switch from feeding to flight from danger. See § 5 of the Timing Devices paper, setting forth the design of a timing devices assembly called a "pulse period selector" that operates like a band-pass filter in electronics, where switching can be controlled by a small variation in a timing interval.
"Brains differ in some rather obvious ways from present-day computers: memory and computation are not separated as they are in all of our current machines; the nervous system operates without any systemwide clock and is built from stochastic elements. Finally, developing as well as mature brains are constantly reprogramming themselves, up or down regulating synaptic weights, modulating the degree of adaptation, shifting the character and frequency of central pattern generators, changing the time constants of integration, and so on. Conceptually, this amounts to the input changing the transition function governing how the machine switches from one state to the next. Put differently, a nervous system will act like a machine that changes its instruction set as a function of its input."Koch's statement is a confusing collection of temporal adjustments that have no inherent basis in a computer model. I do not understand "without any systemwide clock," since I possess at least one in my brain that controls my daily activities like sleep. ["Sleep" is incongruous with a computer model; the "eigen-phase" in Quad Net models (Quad Nets, § 2.c) suggests a reason for sleep, namely, so that neurons can "synchronize their clocks.") In contrast to computers' inability to deal directly with time, levels of temporal adjustment in the Quad Nets model are organized by the inherent design. On the longest time scale, there are adjustments of junctions that correspond to "regulating synaptic weights." Operations can incorporate an inbuilt source of "circadian" or daily rhythms; as well as other rhythmic sources, like sources of musical beats and muscular movements. Inside the daily time scale is a "situational time scale," corresponding, e.g., to movements of a student from home to school to homeroom to math class to physical education to lunch to English class to band practice, etc. Each situation calls for a different distribution of blood flow (energy flow) into the various brain parts. A particular task in a situation calls for fixed signals that will change when the task changes. A shorter time scale involves variations in timing intervals that govern activities of a brain part, like the variations in β and/or δ that control the activities of the 4-cycle, described above. Finally, at the shortest time scale, are the intervals between pulses, e.g., τ=4δ in the 4-cycle.
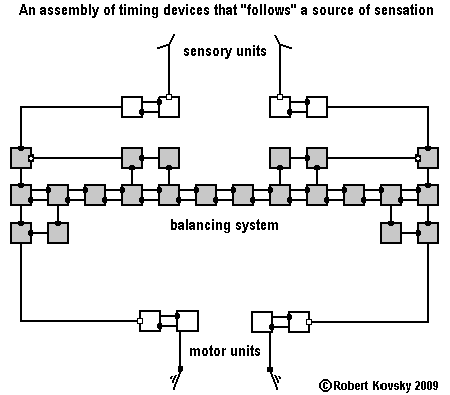
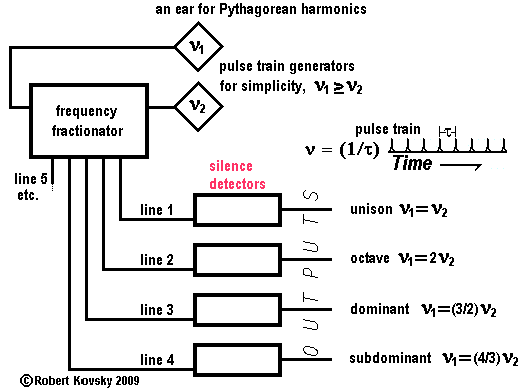
"Although the areas of the brain that respond to individual pitches have been mapped, we have not yet been able to find the neurological basis for the encoding of pitch relations...These relations must be extracted by computational processes that remain poorly understood."Timing device processes can generate pitch relations, but the processes are not computational. This principle is discussed in An Ear for Pythagorean Harmonics: Brain Models Built From Timing Devices (12/28/2009), a web page with a link to a full technical presentation (.pdf file - 460 kB). These advanced developments have grown out of the materials on this website for which there is an earlier version, titled An Ear for Pythagorean Harmonics: Mathematical Processing in Brain Models Built From "Timing Devices," a .pdf file, 212 kB. The image below shows an early design of an Ear for Pythagorean harmonics. When the frequencies of the two input pulse trains are in a specified relation, e.g., the "dominant" relation, a signal appears on the appropriate output. The signal is the result of a "silence" on the appropriate line coming out of the "frequency fractionator." Silences in timing device designs, like engineers' "nulls" and the mathematical "0," are guides and standards of reference. E.g., when the "following" system above is "moving straight ahead directly toward the source of sensation," there are operational silences at pivotal points that are lost when the balance is tilted.
"We know that there are neural circuits specifically related to detecting and tracking musical meter, and we know that the cerebellum is involved in setting an internal clock or timer that can synchronize with events that are out-there-in-the-world."Again, at p.174:
"The cerebellum is the part of the brain that is involved closely with timing and coordinated movements of the body. ... The function of this oldest part of the brain is something that is crucial to music: timing."However, according to Levitin (p. 172):
"The only way we can feel or know these timing variations is if a computational system in the brain is extracting information about when the beats are supposed to occur."
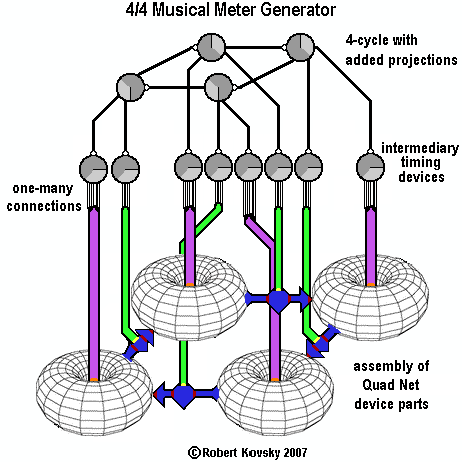 The "4/4 Musical Meter Generator" shown in the adjacent image can generate any 4/4 musical meter within broad operating constraints. It can drive all kinds of muscles, include those that produce breathing, fingerings and tapping feet. No "computational system" is needed. The Generator (shown here as if "dissected" from a full brain) combines the more advanced Quad Nets system with the simpler Timing Devices system, but it is an operational design and potentially realizable. Timing devices make up the 4-cycle previously discussed that is at the top of the image and that provides the basic 4/4 beat (with timing adjustments available for each pulse in the cycle). Additional projections extend downward from the 4-cycle and operate according to the "equal-output rule" discussed in the Timing Devices paper, section 3: when a timing device with multiple projections from produces a pulse, it does so equally through all projections from that timing device.
The "4/4 Musical Meter Generator" shown in the adjacent image can generate any 4/4 musical meter within broad operating constraints. It can drive all kinds of muscles, include those that produce breathing, fingerings and tapping feet. No "computational system" is needed. The Generator (shown here as if "dissected" from a full brain) combines the more advanced Quad Nets system with the simpler Timing Devices system, but it is an operational design and potentially realizable. Timing devices make up the 4-cycle previously discussed that is at the top of the image and that provides the basic 4/4 beat (with timing adjustments available for each pulse in the cycle). Additional projections extend downward from the 4-cycle and operate according to the "equal-output rule" discussed in the Timing Devices paper, section 3: when a timing device with multiple projections from produces a pulse, it does so equally through all projections from that timing device.
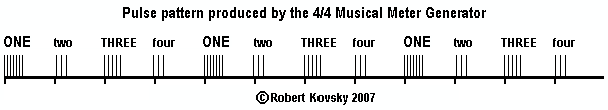
|
( ... ) Opening Page
( ... ) A Kit of Parts ( ... ) An Eye for Sharp Contrast ( ... ) Eyes That Look at Objects ( ... ) An Ear for Pythagorean Harmonics ( ... ) A Procrustean Group of Harmonies ( ... ) Fundamentals of Timing Devices
( ... ) top of this page |
|
( ... ) top of page.
| Your comments and suggestions are welcome. Please write to the adjacent email address (shown in an image to minimize spam). |
|